刘慈欣在他的科幻作品《三体》中，描绘了这样一个概念：当宇宙中更高维度的生命降临地球后，将会对生活在三维世界中的人类造成“降维打击”。这种降维打击是致命的，同时也是完全超出人类想象的。那么，宇宙中真的存在比人类更高维度的生命吗？

什么是维度？

在回答这个问题之前，我们还是要对“维度”这个概念进行一个简单的解释。维度是数学以及物理学中的概念。

在数学中，维度是描述对象状态时所需要使用的独立参数，而在物理学中，维度又摇身一变，成为了系统自由度的数量。

我们又该如何理解维度呢？首先是0维，0维只是一个点，没有长宽高的一个点。当无数的点组成一条线的时候，恭喜你，你就看见了1维——线。

接着，线条连接在一起，框住一个区域，你就得到了拥有长和宽的一个平面，这就是2维世界。

3维则是在面的基础上，拔地而起一个高度，从而形成一个“体积面”，三维空间也正是我们人类现在生活的空间。

在我们的周围，有上下、左右、前后三个空间，这也很好理解，我们可以往哪几个方向移动，就代表我们有哪些空间。

除了这三个空间，我们好像想象不出来该怎么往其他方向上移动了，第四维度真的存在吗？

第四维度

在物理学上，的确存在一个第四维度，它就是时间。与其他三个维度不同，时间是第四维度里唯一的存在，而且时间只能朝着一个方向前进，它只能奔向未来而无法带我们回到过去。

根据物理大师爱因斯坦的说法，我们生活的时空应当是一个四维时空，除了3个空间轴，还有1个时间轴，虽然时间轴是一条虚数值的轴，但整个宇宙都是由时间和空间共同组成的。

那么在数学中，有没有四维空间的存在？当然有，这就不得不提到让数学领先物理100年，甚至可以说是相对论基础的黎曼几何了。

黎曼几何

黎曼认为，既然空间可以是平坦的，那么为什么它们不能是弯曲的呢？于是，黎曼开始研究有曲线的空间，并发现了“正曲率”，平行线在曲面上总会相交，而且三角形的内角之和可以超过180度。

有正的就有负的，黎曼也发现面还可以有“负曲率”，这样，三角形三内角之和还可以小于180度。

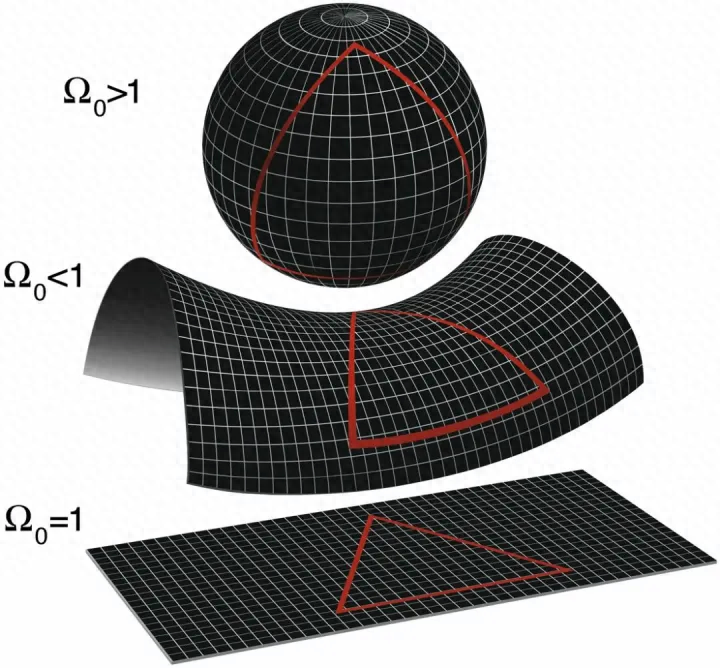
既然面可以弯曲，那两个弯曲的面就可以接触在一起，这时，“黎曼切口”就出现了。

黎曼切口就像沟通多连通空间中的隧道，你可以把宇宙的两个空间想象成两张纸，当它们弯曲碰到彼此时，两张纸连接的地方，就是两个宇宙空间接触的地方。

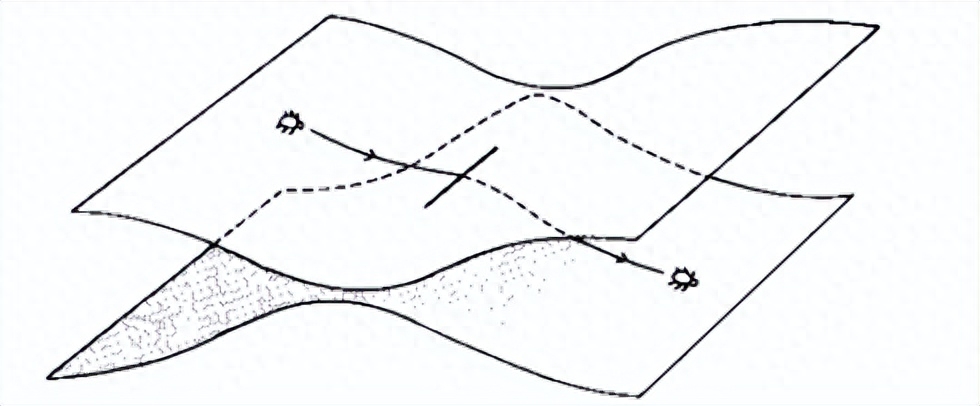
黎曼把这个切口形容成“虫洞”，这和高斯的“书虫”就连接起来了。

这个“书虫”是什么东西？假设在二维平面里生活着一只虫子，即使书面被人类这个高维生物弄得皱巴巴的，在虫子看来，自己的世界依然是平坦的，只不过它们的身体也随着空间变皱了而已。每当它们的身体越过纸上的一道皱纹，它们都会被看不见的“力”影响。

要是两张纸之间打开了一个切口，那么虫子就能通过进出切口，在两个世界之间往返。在虫子看来，这种体验十分神奇又让它困惑，但对于人类来说，事情就像白纸一样简单。

结语

对于虫子来说，空间再怎么改变，在它们的视角里也是平坦的，那么，当人类进入高维空间后，是不是看到的依然是三维世界里的景象呢？

我们的努力在比自己更高维的生物看来，是不是也像虫子一样可笑呢？