前言

“壁虎”古名“守宫”，是一种常栖息于树林、沙漠草原及住宅区等地的爬行纲动物，由于壁虎具有独特的吸附攀爬能力和超强机动性，长期以来，围绕爬壁虎的仿生学研究一直倍受青睐门。

近年来，以壁虎为仿生原型的孵化机械装置和机器人发展迅速，不仅在各行实践作业(如高空勘探、险境救援、环境监测等)中发挥了重要作用，还广泛应用于民用、医学、军事及航天等领域。

我们以爬壁虎的腿足构造及其移动方式为探究方向，提出了一种基于连杆、吸盘和舵机驱动的腿足式仿生关节构型设计方案，并通过仿真分析和实验测试验证了仿生思路及实现方法的可行性，为类壁虎仿生机器人的实践应用提供了有力借鉴。

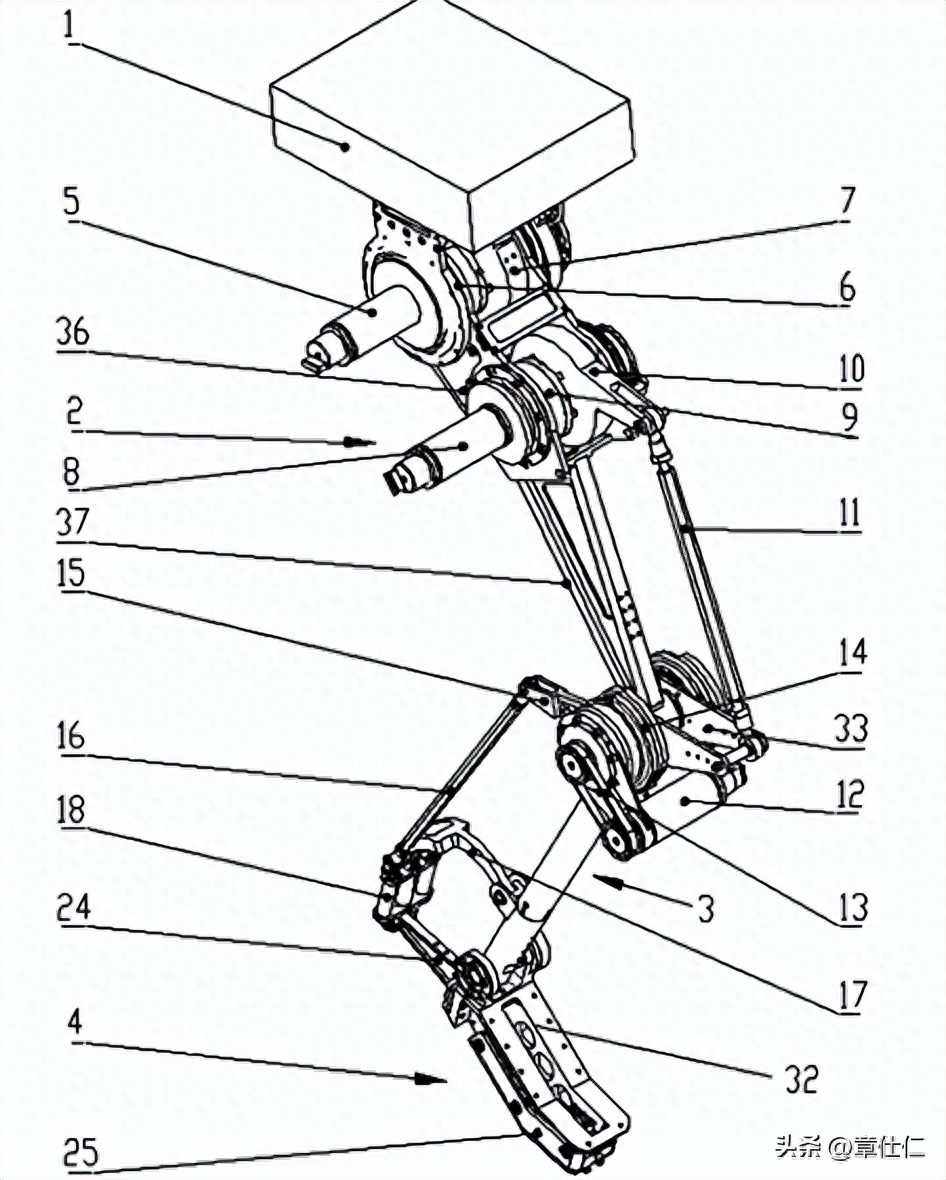
体态特征分析

壁虎昼伏夜出、生性谨慎且反应机敏，危急时刻能够断尾逃生，并且擅捕食蚊、蝇、飞蛾及蜘蛛等，属于有益无害动物。

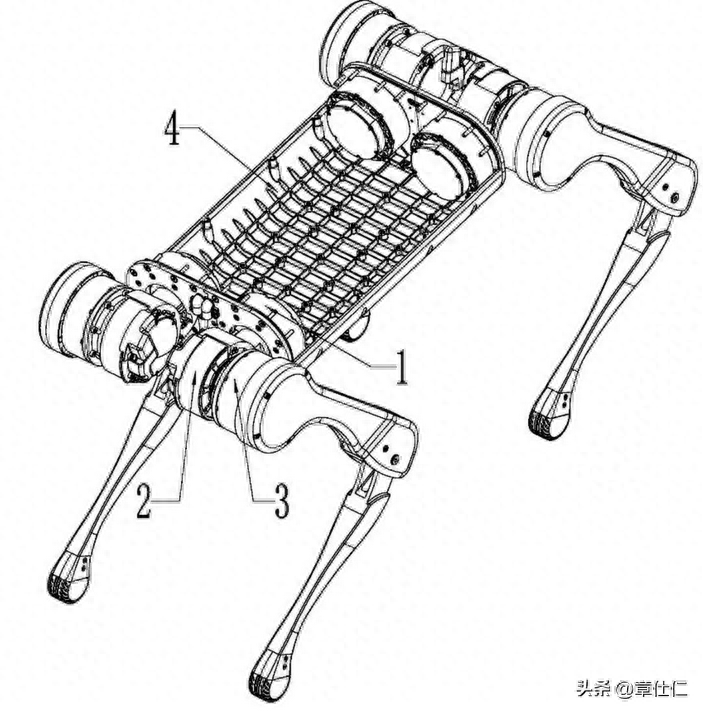
从体态特征来看，壁虎体型微小、背腹扁平，根据腿足关节构造可将其划分为三大模块，即大腿关节、小腿关节及脚趾掌。

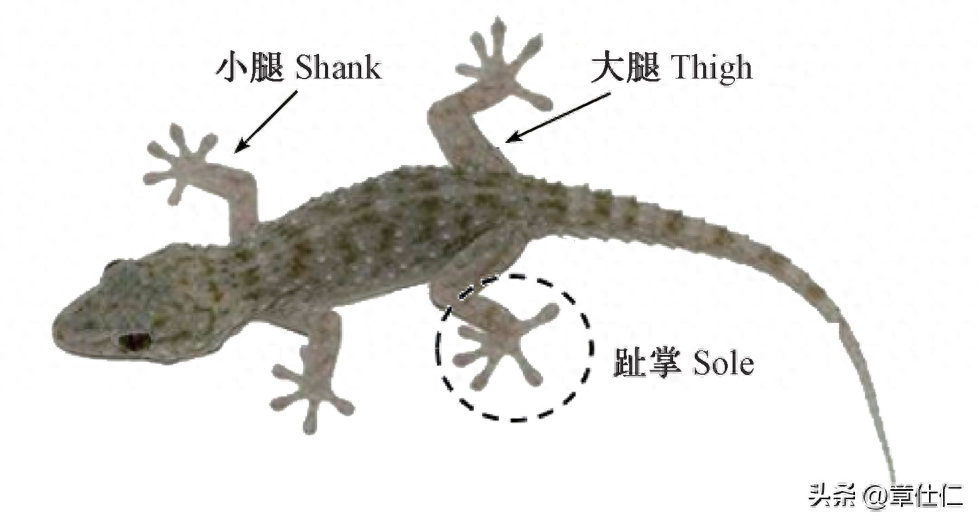
壁虎在移动和攀爬过程中，大腿关节通过前后摆动使小腿关节附带脚掌进行移步换位。

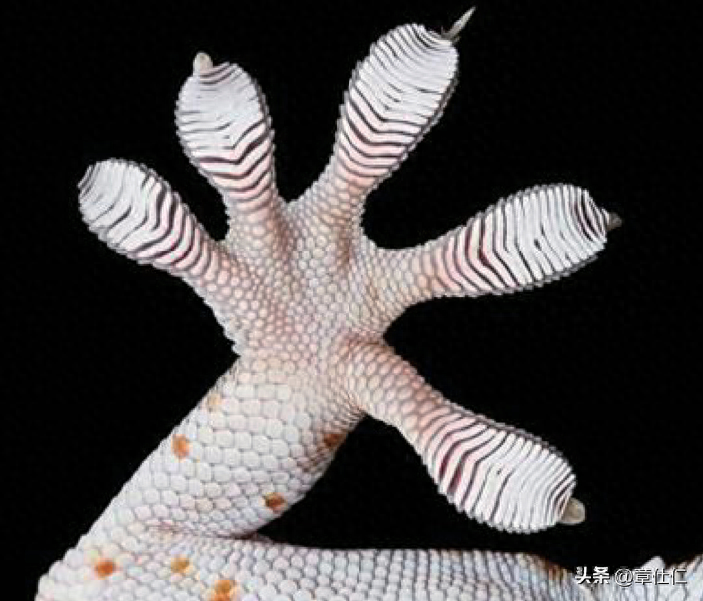
由于壁虎四肢扩展、趾端密布腺毛，这种特殊的生物特征使其趾掌表面具有很强的黏附能力，因此可在光滑壁面、屋檐缝隙、天花板及垂直墙壁上进行吸附停留和自由爬行，在实际吸附或攀爬环境中，为保持躯体平衡和足够黏附力，壁虎至少会有两只脚掌同时与壁面发生接触。

仿生功能构型原理

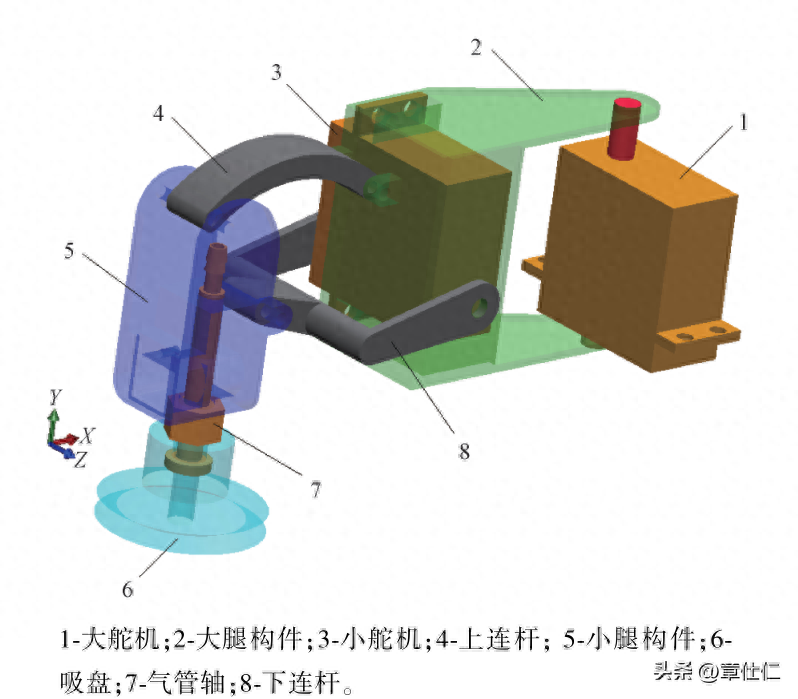
以壁虎腿足关节体态特征为依据，采用连杆、吸盘及舵机等设计其仿生学构型，该构型由舵机1舵机2联合驱动，其运行原理为：

大腿构件在机1驱动下绕Y轴发生一定角度摆动，与此同时，舵机2通过下连杆将动力传递至小腿构件和上连杆，使其附带吸盘分别绕C点和D点发生一定角度摆动，由此实现仿生壁虎的爬行运动。

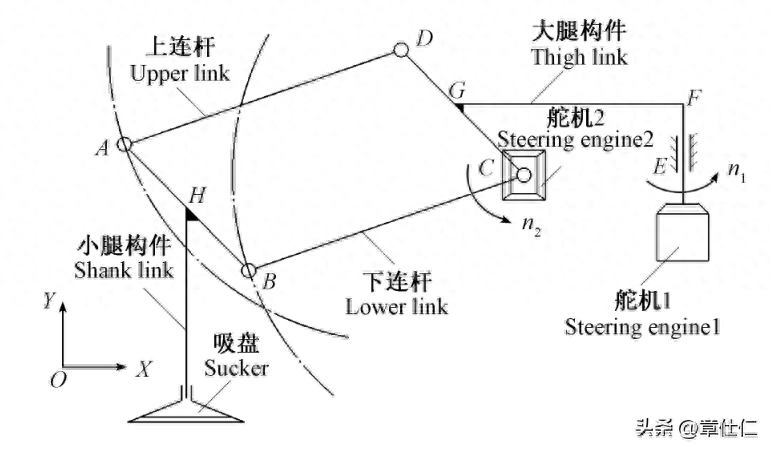
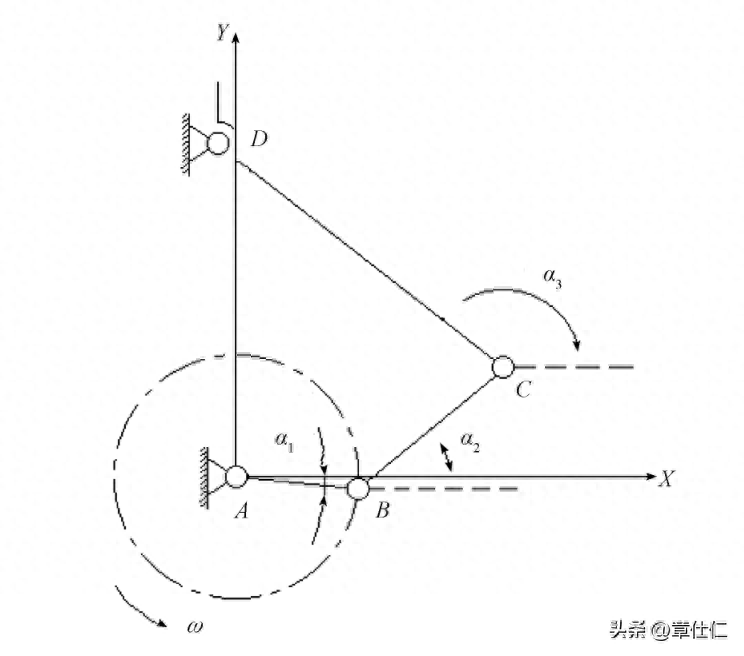
由机构学分析可知，壁虎的移步换位可认为是两种运动模式的耦合，即大腿关节在XOZ面内的摆动前行和小腿关节在XOY面内的升降运动。

考虑到腿足关节的传动稳定性，采用平行四边形机构(ABCD)作为大、小腿关节之间的过渡连接，其中，大腿关节与CD杆刚性固接，小腿关节与AB杆刚性固接，且有 Lab=Lcd=33 mm，LaD =LBc=49 mm。

平行四边形机构是特殊的双曲柄机构，由于两个曲柄的长度以及转速、转向均相同，因此该机构无急回特性，有利于仿生关节的姿态协调与平稳运动。

仿生造型

仿生造型设计是一种常用的产品造型手法，与产品形态相关的仿生设计包括形态仿生、功能仿生结构仿生及色彩仿生等。

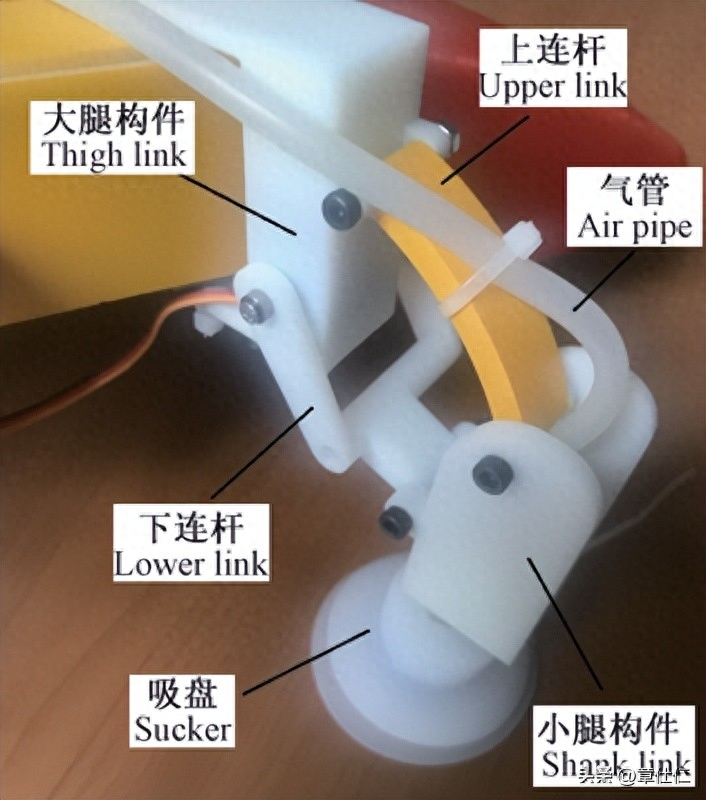
以腿足关节的功能构造为参考，通过仿生学形态分析和结构表达，对其主要构成元素进行造型设计，下图为上连杆、下连杆、吸盘、大腿关节及小腿关节在SolidWorks环境下的三维实体造型，这种基于特征的仿生造型能够方便、快捷地响应修改需求，有助于提高仿生关节的建模效率和造型可塑性。

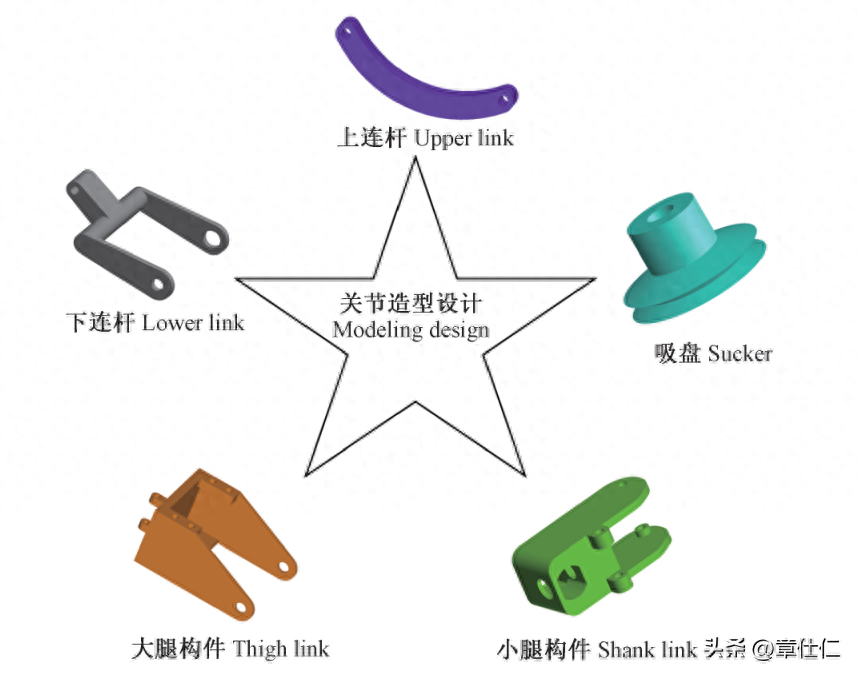
为保证腿足关节的仿生设计精度，需要严格控制零部件之间的约束关系与配合尺寸，同时根据体、面、线等干涉检验结果对造型特征加以优化，以避免仿生关节出现死点或碰撞。

此外，在对各构件进行仿生造型设计时，在满足功能要求的前提下应尽量使其结构轻巧、造型美观。

机构学设计

由机构学理论可知，仿生关节构型的机动动作主要取决于平面四杆机构的尺寸及其组合形式，由于平行四边形机构属于特殊的平面四杆机构，故可按照一般四杆机构推导其运动学方程。

根据平面机构矢量封闭原则，各杆件之间存在矢量关系：LaB + LBc = LcD +LaD

将式(1)等号两边矢量分别沿 X 轴、Y轴进行投影，得到如式(2)所示平面机构位移方程：

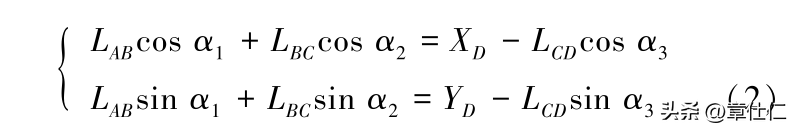
式中，a1、a2、a3;分别为AB 杆、BC杆、CD杆与X轴正向夹角，Xd、Yd分别为D点在X轴和Y轴上的坐标。

以时间 t 为变量，对式(2)进行一阶求导数，即得到机构速度方程：

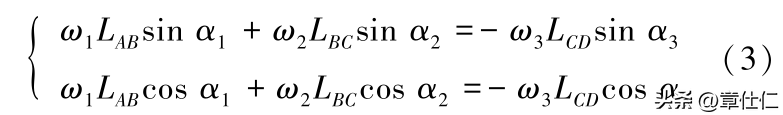
式中，w1、w2、w3分别为AB杆、BC杆、CD杆的质心角速度。

同理，对式(3)中的时间变量再次求导，便可获得平面四杆机构的加速度方程，对于平行四边形机构将等边关系(Las=Lcd，Lbc=Lad)代入式(2)后，通过对时间变量t进行一阶求导和二阶求导，便可得到对应的速度方程和加速度方程。

为验证腿足关节机构学设计的可行性，利用Adams/View构建其动力学仿真模型。

由大小腿关节构造形式可知，该模型是一套具有典型连杆特征的平面机械组件，因此，可按式(4)计算其机构自由度：F=3n - 2PL- PH

分析机构组成可知，该仿生关节包含的活动构件数目n=4，低副数目PL=5高副数目PH=0，并且不存在虚约束和局部自由度。

将各变量值代入式(4)计算得出机构自由度F=2，由于仿生关节采用两路舵机联合驱动，即机体具有两个原动件，所以自由度计算结果符合机构学条件。

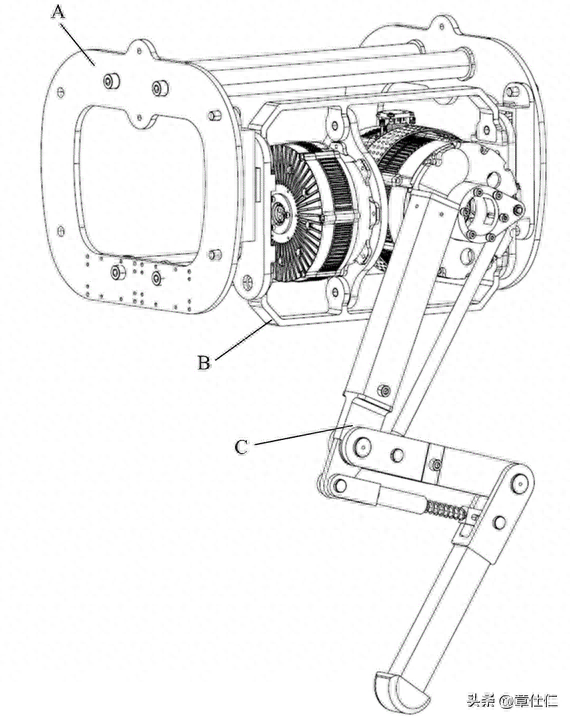
在运动约束定义基础上，分别对舵机1(MG996R)和舵机2(MG90S)施加基于step函数的 Motion驱动，由于舵机反应转速区间为53 r/min ~62r/min，所以将电动机输出轴转速设定为360 deg/s，并通过舵机轴正反转控制来实现大、小腿关节的独立驱动。

考虑到仿生关节的机构尺寸和运动极限，设定上连杆最大摆动角度为43°，下连杆最大摆动角度为 73°，并据此构建控制大、小腿关节正反转的step函数q1(t)和q2(t)：

根据壁虎步态特点，可将腿关节运动分解为抬起、迈步、落下三个动作，其中，舵机2控制小腿关节进行抬和落，舵机1控制大腿关节进行迈步摆动。

对仿生壁虎的大、小腿关节进行联动仿真。

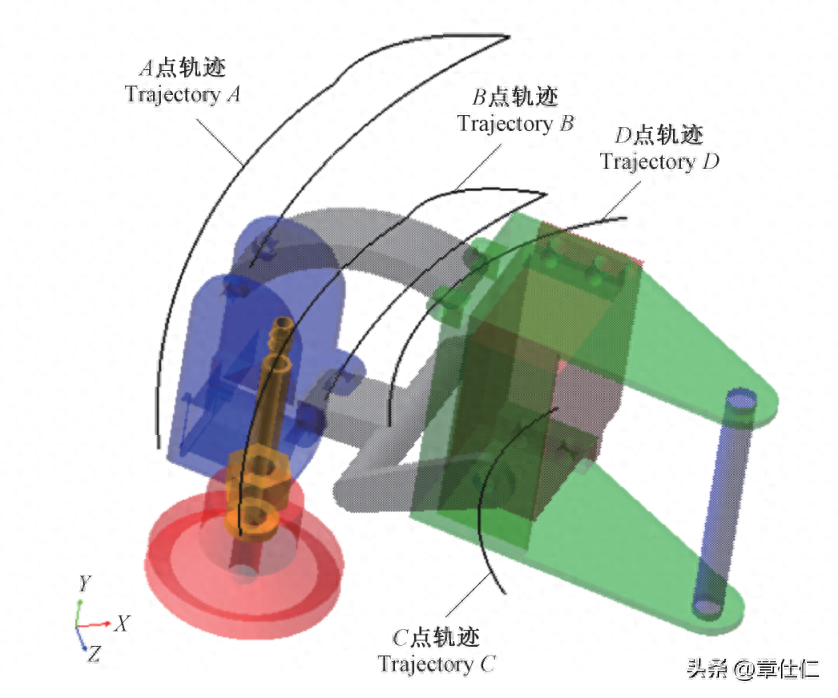
十分明显，在腿关节的抬、迈、落机动过程中，各关键动点(A、B、C、D)的运动轨迹光滑清晰、过渡平缓，且相互之间无交叉与重合。

这说明腿部关节构造合理，运动与传力过程平稳可靠，具有良好的仿生动力学性能。

角运动规律

由腿足关节构造可知，A点与小腿关节相连，C点与大腿关节相连，因此，可通过A点和C点的仿真曲线来表征小腿关节和大腿关节的运动学特性。

在后处理模块提取A点运动学曲线，A点摆动角度区间为0~43°，通过起始位置测量得知，小腿关节抬升高度约33.6 mm，因此该仿生关节能够跨越的障碍物高度在30 mm左右。

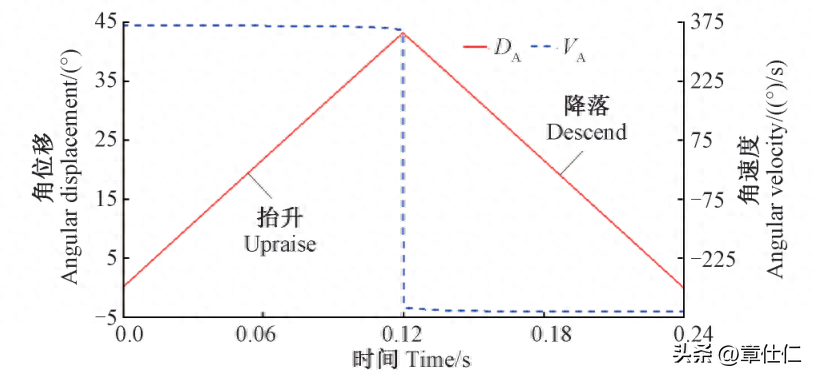
同样通过后处理获取C点运动学曲线，测量得出大腿关节(C点)摆动角度区间为 0~73°，可见，大腿关节的前摆和后摆幅度相对较大，能够满足仿生壁虎的移步换位要求。

由 A 点和 C点的运动学仿真曲线可知，小腿关节在0.1194 s时发生升降切换，最大摆动角度为43°，大腿关节在0.2028s时发生正反转切换最大摆动角度为73°，这与step函数的 Motion驱动计算完全相符。

此外，由于大、小腿关节的驱动电动机都匀速输出[360(°)/s]，所以加速度为0，从角速度曲线形态来看，A点和C点的运动过程没有波动和冲击，说明角速度与角加速度仿真结果符合step函数设计预期。

综上可知，大、小腿关节联动运行平稳，且在抬、迈、落机动过程中无急回特性，符合平行四边形机构学条件。

静力学计算与分析

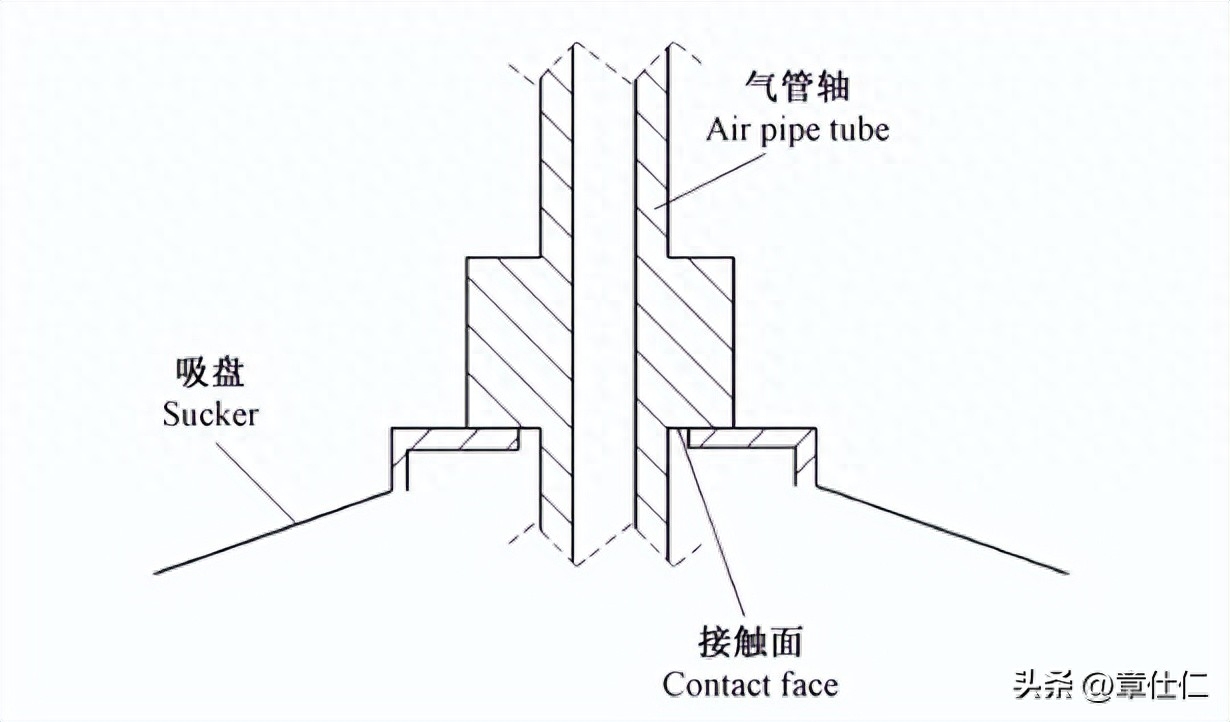
对腿足关节构造进行简化处理，由于真空吸盘主要承受气动负压作用，静力学分析时可将吸盘内部的吸附力等效转化至气管轴，故建模过程忽略吸盘影响。

在Workbench环境下建立有限元模型，采用六面体实体单元Solid186和四面体实体单元 Solid187进行结构离散，并在细小特征及其接触区域进行局部网格加密。

该模型是一种多体形式的结构组件，其中气管轴为钢质构件，大腿关节、小腿关节、上连杆和下连杆均为3D打印构件，材质采用高强度光敏树脂。

根据腿部实际自由度状态和承载条件定义边界条件，各连接构件之间采用实体面组绑定接触。

在上、下连杆与大、小腿关节铰接处分别定义圆柱副约束，由于所采用的舵机均为单轴动力输出，且最大驱动扭力分别为T1=13 kgcm和T2 =kg·cm。

因此，考虑到关节安全裕度，按照最大扭力定义边界条件，即在大腿关节与舵机1铰接处沿 Y轴正向定义转矩T1，同时在下连杆与舵机2铰接处沿Z轴正向定义转矩T2。

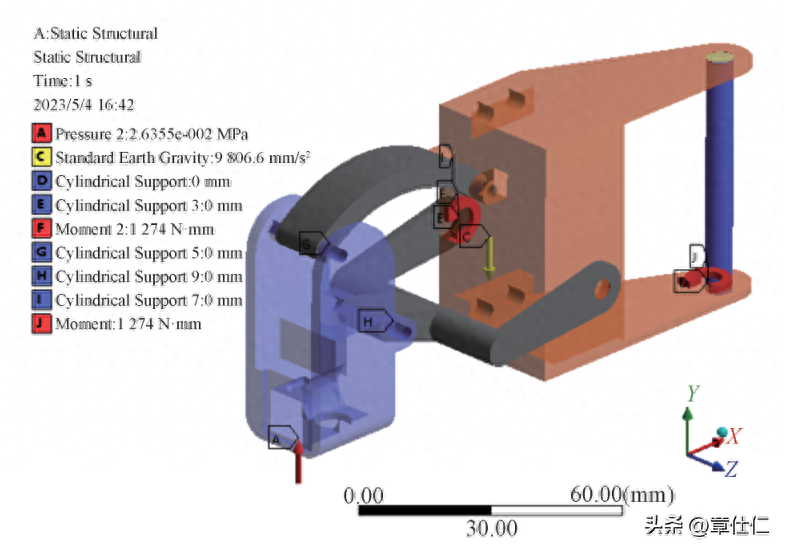
当仿生机体支撑于平地时会在腿足关节产生反向作用力，为便于分析计算，可将吸盘与气管轴的接触面看作支撑面，支撑面的面积s=99.03 mm。

为保持躯体平衡，仿生壁虎在爬行过程中至少应保持两只脚掌同时着地，因此可按式(4)计算作用于单腿支撑面的反向压力P1。

已知机体质量m=1.75 kg，重力加速度 g为9.8m/s，代入式(7)计算得出P1=86 589.92 Pa。

同理，当仿生壁虎在天花板吸附爬行时，需要克服机体自重到挂吸附于天花板之上，此时，作用于支撑面的最小吸附压力P2，与平地支撑时的P1大小相等、方向相反。

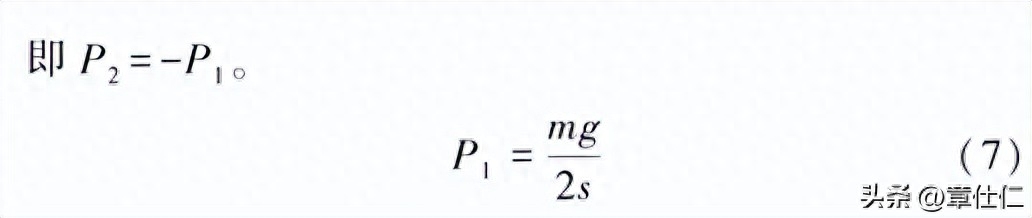
仿生壁虎在垂直壁面上吸附攀爬时，吸盘与墙壁之间的最大静摩擦力必须大于机体自重，因此，可按式(8)计算最小吸附力Wmin，已知静摩擦因数u=0.45，则代入式(8)计算得出W =38.11 N。

在此基础上，可由式(9)计算出作用于单腿支撑面的最小吸附压力P3=192416.44 Pa。

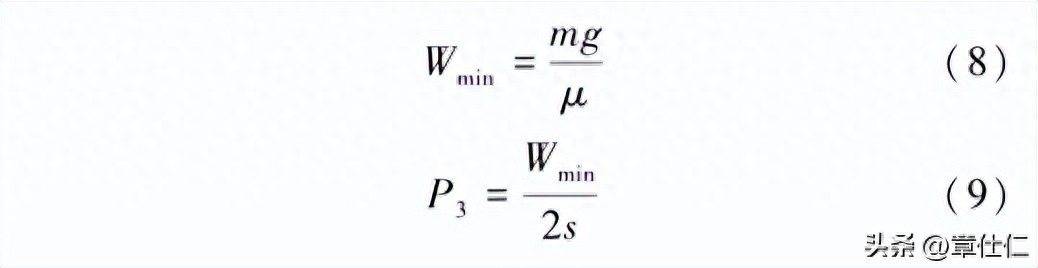
应力与变形

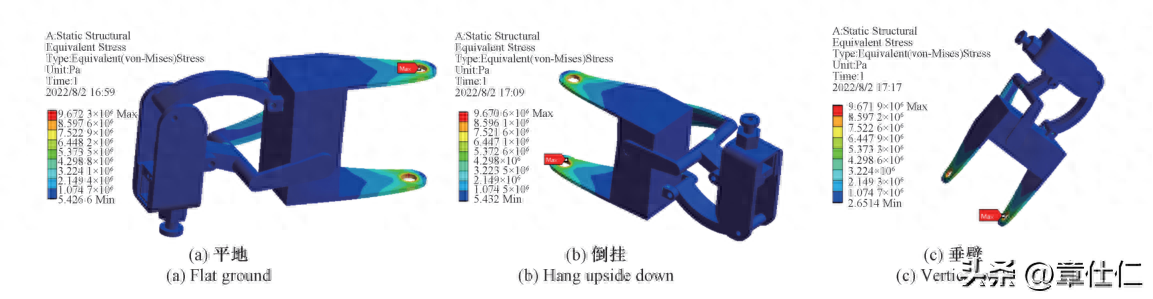
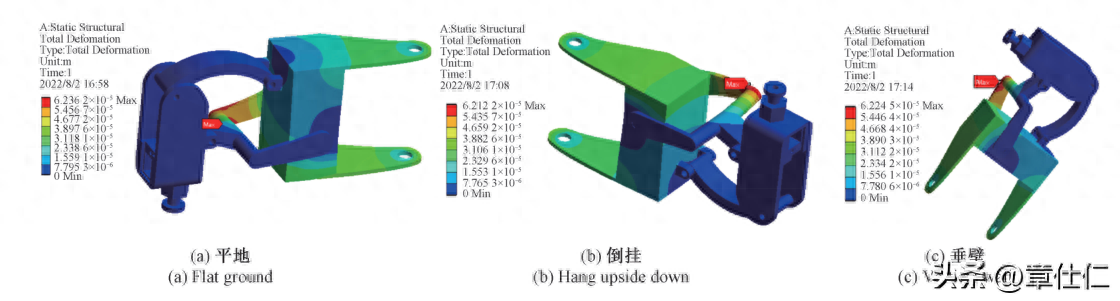
在三种承力状态(平地、倒挂和垂壁)下对腿足关节进行有限元静力学分析，分析对比可知，三种状态下的最大von-Mises应力十分接近，且均出现在大腿关节与舵机1饺接区域附近。

其中，平地支撑时产生的极限von-Mises应力最大(9.6723MPa)，垂壁吸附次之(9.6719 MPa)，倒挂吸附最小(9.6706 MPa)，由此可知，当有两条腿关节同时起支撑吸附作用时，平地、倒挂和垂壁三种状态下的应力分布状态基本相当最大应力o均在9.67 MPa 左右。

大腿关节采用光固化3D打印工艺制成，已知光敏树脂的拉伸强度为50~60 MPa，弯曲强度为75~110 MPa。

根据最大von Mises应力准则如式(10)所示，比较可知，最大应力om远小于树脂材料的屈服强度[8imn]，说明仿生关节具有足够的强度储备。

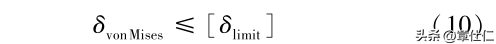
通过分析比较关节组件的静力变形云图可知，三种承力状态下的最大变形均发生于下连杆横轴端部区域，且最大形变量d从大到小依次为62.362 (平地)、62.245 (垂壁)、62.122 um(倒挂)。

十分明显，最大变形幅度非常微小(约62μm)，不会对下连杆的结构刚度产生破坏性影响，因此关节的静力变形符合刚度设计要求。

实验测试

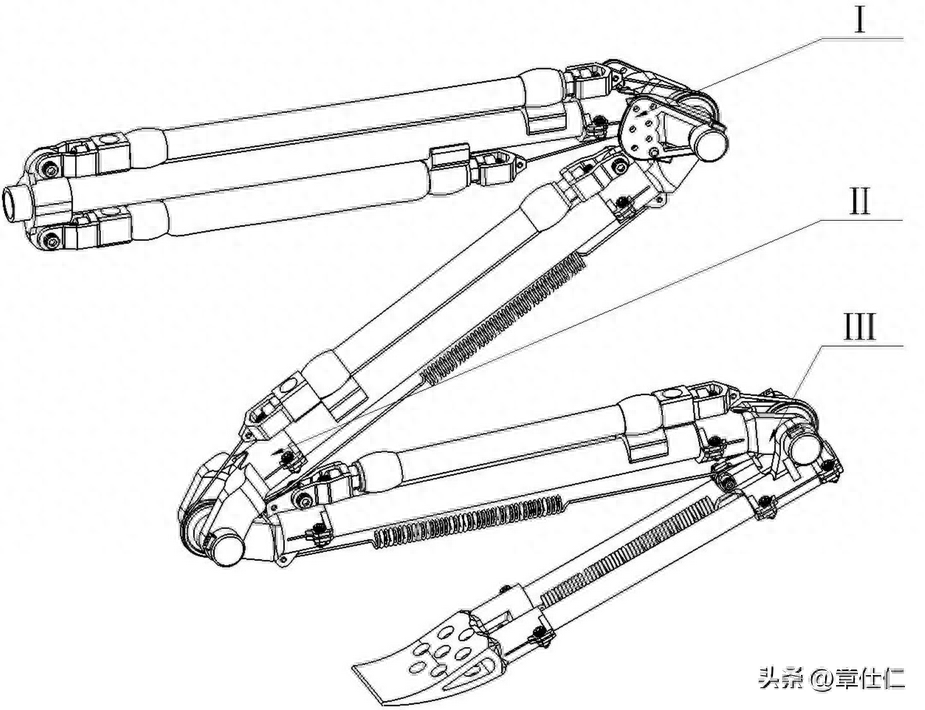
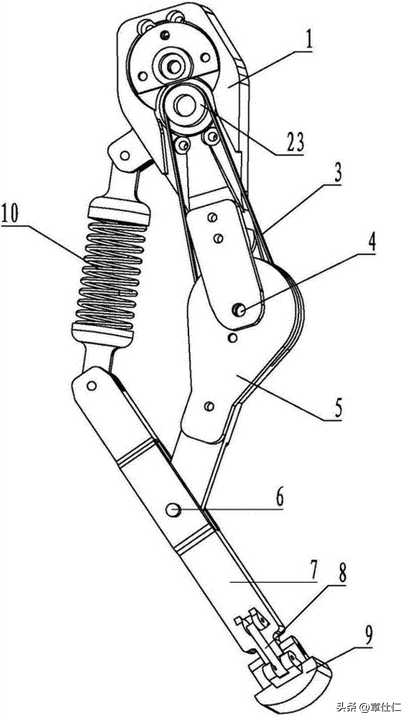
制作仿生移动关节构型组件模块时，大、小腿关节及连杆构件等均采用光固化3D打印工艺制成，按照仿生关节构型关系进行调试组装，各运动构件之间采用销钉连接。

考虑到机体实际结构空间布局及尺寸限制，选用直径为50 mm的橡胶材质真空吸盘，同时由负压为-55 kPa的真空发生器提供负压吸力，并通过电磁阀控制和软管输送至吸盘。

在各功能模块开发基础上，试制仿生机械壁虎实验样机，并对其移动关节的机动性和可靠性进行实验测试。

为避免大小腿关节发生死点或碰撞，理论层面的各项参数均留有一定控制冗余度，而实际测试参数则根据机体机动情况进行设定和选择。

参数的理论区间均包含在实验区间内，说明仿生关节可在安全运行空间内满足自身功能设计要求。

不同环境下的实验测试表明，仿生壁虎腿足关节运动平稳、传力可靠舵机驱动能够快速响应机体对于移步换位的机动要求，并且在步态变换过程中，四组仿生关节构型的位姿表现协调一致，体现出良好的仿生动力学特性，各项实验指标达到设计预期。

结语

以爬壁虎原型为参考，在机构分析、理论计算、仿真设计及实验验证基础上，提出了一种腿足式仿生移动关节的设计思路及实现方法。

通过将连杆、舵机、真空吸盘等应用于腿足关节构型，在实现仿形设计的同时，显著增强了仿生移动关节的机动性与可靠性，具有可期的技术发掘潜力和实践应用价值。

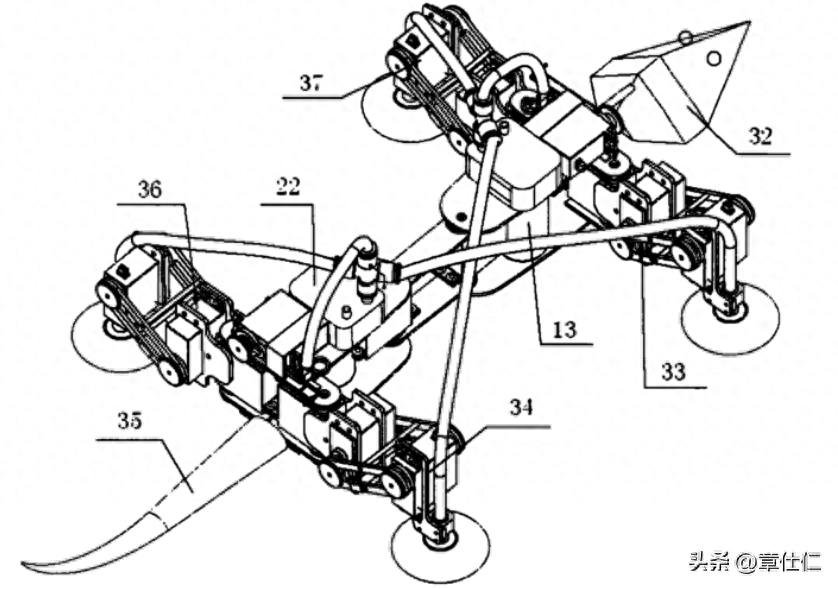
相对于其他类型的仿生关节，这种基于连杆构型的两自由度移动关节，不但设计轻巧、构型简单，而且能在很大程度上提升仿生机体的机动性与越障能力，有助于爬行纲仿生关节的设计创新。